Question

You find 72 coins consisting only of nickels, dimes, and quarters, with a face value of $10.20. However, the coins all date from 1919, and are worth considerably more than their face value. A coin dealer offers you $10 for each nickel, $20 for each dime, and $15 for each quarter, for a total of $1,060. How many nickels did you find?

Answer 1

You have found 24 nickels.

Explanation:

Let N be the number of nickles, D be the number of dimes and Q be the number of quarters. The number of coins and their face values are given by the following expressions, respectively:

`N+D+Q=72\\0.05N+0.10D+0.25Q=10.20`

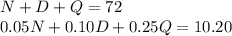
As of now we have three variables and two expressions, the final expression needed to solve the linear system is given by the amount offered by the coin dealer:

`10N+20D+15Q=1,060`

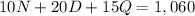
Solving the linear system:

`N+D+Q=72\\5N+10D+25Q=1,020\\10N+20D+15Q=1,060\\\\10N-10N+20D-20D+15Q-50Q=1,060-(2*1,020)\\-35Q=-980\\Q=28\\\\5N-10N+10D-10D+25Q-10Q=1,020-720\\-5N+15Q=300\\-5N=300-(15*28)\\N=24`

You have found 24 nickels.