Answer:
The final angular speed of the merry-go-round is
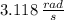
 .
.
Step-by-step explanation:
Given the absence of external forces, the final angular speed of the merry-go-round can be determined with the resource of the Principle of Angular Momentum Conservation, which is described in this case as:
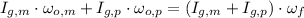
Where:
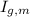 - Moment of inertia of the merry-go-round with respect to its axis of rotation, measured in
- Moment of inertia of the merry-go-round with respect to its axis of rotation, measured in
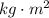 .
.
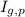 - Moment of inertia of the person with respect to the axis of rotation of the merry-go-round, measured in
- Moment of inertia of the person with respect to the axis of rotation of the merry-go-round, measured in
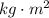 .
.
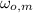 - Initial angular speed of the merry-go-round with respect to its axis of rotation, measured in radians per second.
- Initial angular speed of the merry-go-round with respect to its axis of rotation, measured in radians per second.
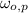 - Initial angular speed of the merry-go-round with respect to the axis of rotation of the merry-go-round, measured in radians per second.
- Initial angular speed of the merry-go-round with respect to the axis of rotation of the merry-go-round, measured in radians per second.
 - Final angular speed of the merry-go-round-person system, measured in radians per second.
- Final angular speed of the merry-go-round-person system, measured in radians per second.
The final angular speed is cleared:

Merry-go-round is modelled as uniform disk-like rigid body, whereas the person can be modelled as a particle. The expressions for their moments of inertia are, respectively:
Merry-go-round
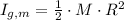
Where:
 - The mass of the merry-go-round, measured in kilograms.
- The mass of the merry-go-round, measured in kilograms.
 - Radius of the merry-go-round, measured in meters.
- Radius of the merry-go-round, measured in meters.
Person

Where:
 - The mass of the person, measured in kilograms.
- The mass of the person, measured in kilograms.
 - Distance of the person with respect to the axis of rotation of the merry-go-round, measured in meters.
- Distance of the person with respect to the axis of rotation of the merry-go-round, measured in meters.
If
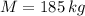 ,
,
 ,
,
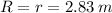 , the moments of inertia are, respectively:
, the moments of inertia are, respectively:
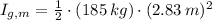
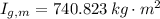
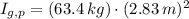
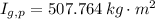
The angular speed experimented by the person with respect to the axis of rotation of the merry-go-round is:
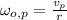
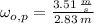
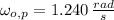
Given that
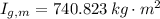 ,
,
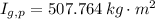 ,
,
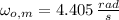 and
and
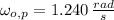 , the final angular speed of the merry-go-round is:
, the final angular speed of the merry-go-round is:
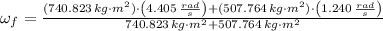
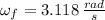
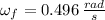
The final angular speed of the merry-go-round is
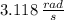
 .
.