The question is incomplete. Here is the complete question.
A organizational psychologist measures levels of job satisfaction in a sample of 30 participants. To measure the variance of job satisfaction, it is calculated that the SS = 120 for this sample.
What are the degrees of freedom for the variance?
Compute the variance and standard deviation.
Answer: Degrees of freedom = 29
Variance = 4.138
Standard Deviation = 2.034
Step-by-step explanation: Degrees of freedom is a number of values in calculation of statistics that are free to vary, i.e., in how many ways a system can move independently. To determine it:
df = n - 1
which n is the quantity of the sample or population
For this sample: df = 30 - 1 = 29
The degrees of freedom is 29.
SS is the sum of the squared deviation, i.e., ∑(x - mean)².
Variance is calculated as:
variance = ∑(x - mean)² / n - 1 = SS / n - 1
variance =

variance = 4.138
Standard deviation is the spread from the mean and is the square root of variance:
standard deviation =
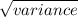
standard deviation =
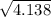
standard deviation = 2.034