Question

A box at rest has the shape of a cube 2.6 m on a side. This box is loaded onto the flat floor of a spaceship and the spaceship then flies past us with a horizontal speed of 0.80c. What is the volume of the box as we observe it

Answer 1

The observed volume of the box is 3.796 cubic meters.

Step-by-step explanation:

The observed length is determined by the formula for the Length Contraction:

`L = (L_(o))/(\gamma)`

Where:

`L` - Proper length, measured in meter.

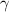`\gamma` - Lorentz factor, dimensionless.

The Lorentz factor is represented by the following equation:

`\gamma = \frac{1}{\sqrt{1-(v^(2))/(c^(2)) }}`

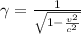
If
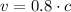`v = 0.8\cdot c`, then:

`\gamma = \frac{1}{\sqrt{1-(0.64\cdot c^(2))/(c^(2)) }}`

`\gamma = (1)/(√(1-0.64))`

`\gamma = (5)/(3)`

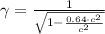
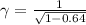
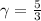
Therefore, the observed length is:

`L = (3)/(5)\cdot L_(o)`

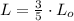
Given that
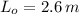`L_(o) = 2.6\,m`, the observed length is:

`L = (3)/(5)\cdot (2.6\,m)`

`L = 1.56\,m`

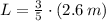
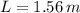
The observed volume of the box is:

`V = L^(3)`

`V = (1.56\,m)^(3)`

`V= 3.796\,m^(3)`

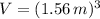
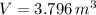
The observed volume of the box is 3.796 cubic meters.