Question

A 1.40-kg block is on a frictionless, 30 ∘ inclined plane. The block is attached to a spring (k = 40.0 N/m ) that is fixed to a wall at the bottom of the incline. A light string attached to the block runs over a frictionless pulley to a 60.0-g suspended mass. The suspended mass is given an initial downward speed of 1.40 m/s . Part A How far does it drop before coming to rest? (Assume the spring is unlimited in how far it can stretch.)

Answer 1

the mass drop by 6.5cm before coming to rest.

Step-by-step explanation:

Given that:

the mass of the block M= 1.40 kg

angle of inclination θ = 30°

spring constant K = 40.0 N/m

mass of the suspended block m = 60.0 g = 0.06 kg

initial downward speed = 1.40 m/s

The objective is to determine how far does it drop before coming to rest?

Let assume it drops at y from a certain point in the vertical direction;

Then :

Workdone by gravity on the mass of the block is:

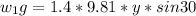`w_1g = 1.4*9.81*y*sin30` = - 6.867y

Workdone by gravity on the mass of the suspended block is:

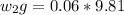`w_2g = 0.06*9.81` = 0.5886

The workdone by the spring = -1/2ky²

= -0.5 × 40y²

= -20 y²

The net workdone is = -20 y² - 6.867y + 0.5886y

According to the work energy theorem

Net work done = Δ K.E

-20 y² - 6.867y + 0.5886 = 1/2 × 0.06 × 1.4²

-20 y² - 6.867y + 0.5886 = 0.5 × 0.1176

-20 y² - 6.867y + 0.5886 = 0.0588

-20 y² - 6.867y + 0.5886 - 0.0588

-20 y² - 6.867y + 0.5298 = 0

multiplying through by (-)

20 y² + 6.867y - 0.5298 = 0

Using the quadratic formula:

`(-b \pm √(b^2-4ac))/(2a)`

where;

a = 20 ; b = 6.867 c= - 0.5298

`(-(6.867) \pm √((6.867)^2-(4*20*-0.5298)))/(2*(20))`

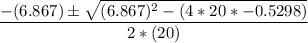
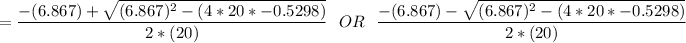`= (-(6.867) + √((6.867)^2-(4*20*-0.5298)))/(2*(20)) \ \ \ OR \ \ \ (-(6.867) - √((6.867)^2-(4*20*-0.5298)))/(2*(20))`= 0.0649 OR −0.408

We go by the positive integer

y = 0.0649 m

y = 6.5 cm

Therefore; the mass drop by 6.5cm before coming to rest.