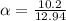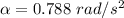Question

Two blocks are placed at the ends of a horizontal massless board, as in the drawing. The board is kept from rotating and rests on a support that serves as an axis of rotation. The block on the right has a mass of 4.4 kg. Determine the magnitude of the angular acceleration when the system is allowed to rotate.

Answer 1

The angular acceleration is
`\alpha = 0.788 \ rad/s^2`

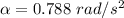
Step-by-step explanation:

The diagram for this question is shown on the first uploaded image (gotten from study website)

From the question we are told that

The mass of the block on the right is
`m_r = 4.4 \ kg`

The mass of the block on the left is
`m_l = 12 \ kg`

The distance of the left mass to the center is
`r_l = 0.6 \ m`

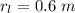
The distance of the right mass to the center is
`r_l = 1.4 \ m`

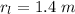
At the point the system is allowed to rotate the upward torque is mathematically evaluated as

`\tau = m_l * g * r_l - m_r * g * r_r`

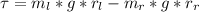
substituting values

`\tau = 12 * 9.8 * 0.6 - 4.4 * 9.8 * 1.4`

`\tau = 10.2 \ N m`

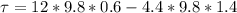
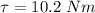
The moment of inertia of the system is mathematically represented as

`I = m_l r_l ^2 +m_r r_r^2`

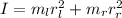
substituting values

`I = 12 * (0.6)^2 +(4.4)* (1.4)^2`

`I = 12.94 \ kg \cdot m^2`

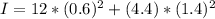
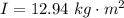
The angular acceleration is mathematically represented as

`\alpha = (\tau)/(I)`

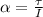
substituting values

`\alpha = (10.2)/(12.94)`

`\alpha = 0.788 \ rad/s^2`