Answer:
a) The baseball spends 0.674 seconds in the air
b) The horizontal distance from the roof edge to the point where the baseball lands on the ground = 2.02 m
Step-by-step explanation:
The ball's initial speed, u = 3.8 m/s
θ = 38°
The edge of the roof has a height, H = 3.30 m
The vertical motion of the baseball can be given by the equation:
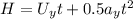 .........(1)
.........(1)
Vertical acceleration of the baseball,
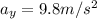
The vertical component of the initial speed can be calculated by:
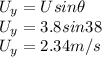
Substituting the appropriate values into equation (1):

Solving for t in the quadratic equation above:
t = 0.674 s
To calculate the horizontal distance, S, use the formula below:
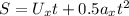
Horizontal acceleration of the baseball,
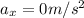
The horizontal component of the initial speed can be calculated as:

S = 2.99(0.674) + 0.5(0)
S = 2.02 m