Question

3. According to a survey, 68% of Americans say that

they go to a movie theater at least once a month.
Suppose that this proportion is true for the current
American population.
a.
Let x be a binomial random variable that denotes
the number of Americans in a random sample of
12 who say that they go to a movie theater at
least once a month. What are the possible
values that x can assume?
b. Find the probability that exactly 9 Americans in
a random sample of 12 will say that they go to a
movie theater at least once a month.

Answer 1

The probability that exactly 9 Americans in a random sample of 12 will say that they go to a movie theater at least once a month

P( X = 9) = 0.007343

Explanation:

Step(i):-

According to a survey, 68% of Americans say that they go to a movie theater at least once a month.

Given proportion 'p' = 68% =0.68

q = 1-p = 1- 0.68 = 0.32

Given Number of Americans in a random sample

'n' = 12

Let 'X' be random variable of binomial distribution

`P( X = r) = n_{C_(r) } p^(r) q^(n-r)`

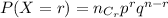
Step(ii):-

Given r = 4

Given random sample 'n' =12

The probability that exactly 9 Americans in a random sample of 12 will say that they go to a movie theater at least once a month

`P( X=9) = 12_{C_(9) }( 0.68)^(9) (0.32)^(12-9)`

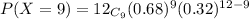
using factorial notation

`12 C_(9) = 12_{C_(12-9) } = 12_{C_(3) } = (12!)/((12-3)!3!) = (12 X 11 X 10 X 9!)/(9!3 X 2 X 1) = (12 X 11 X 10)/(3 X 2 X 1) = 220`

`P( X=9) = 220( 0.68)^(9) (0.32)^(12-9)`

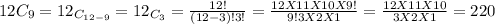
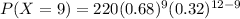
On calculation , we get

P( X = 9) = 0.007343

Final answer:-

The probability that exactly 9 Americans in a random sample of 12 will say that they go to a movie theater at least once a month

P( X = 9) = 0.007343