Question

A high school runs a survey asking students if they participate in sports. The results are found below. Run an independence test for the data at α=0.01. Freshmen Sophomores Juniors Seniors Yes 75 88 55 42 No 30 28 38 40 Can it be concluded that participation in sports is dependent on grade level?

Answer 1

It can be concluded that participation in sports is dependent on grade level.

Explanation:

In this case a Chi-square independence test for the data is to be performed at α = 0.01.

The hypothesis can be defined as follows:

H₀: The participation in sports is independent of grade level.

Hₐ: The participation in sports is dependent of grade level.

The data provided is:

Freshmen Sophomores Juniors Seniors

Yes 75 88 55 42

No 30 28 38 40

The formula to compute the expected frequencies is:

`E_(i)=\frac{i^(th)\ \text{Row Total}\ *\ i^(th)\ \text{Column Total}}{N}`

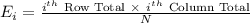
The Chi-square statistic is:

`\chi^(2)=\sum {((O_(i)-E_(i))^(2))/(E_(i))}`

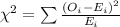
Consider the Excel file attached below.

The value of Chi-square statistic is 16.244.

The degrees of freedom of the test are:

`\text{df}=(r-1)(c-1)`

`=(4-1)(2-1)\\=3* 1\\=3`

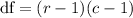
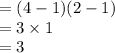
Compute the p-value of the test as follows:

`p-value=P(\chi^(2)_(df)<\chi^(2))`

`=P(\chi^(2)_(3)<16.244)\\=0.001`

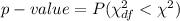
*Use a Chi-square table.

p-value = 0.001 < α = 0.01

The null hypothesis will be rejected at 1% level of significance.

Thus, it can be concluded that participation in sports is dependent on grade level.