Question

Find the missing number in the pattern! PLEASE HELP The half-life of caffeine is 5 hours; this means that approximately 1/2 of the caffeine in the bloodstream is eliminated every 5 hours. Suppose you drink a 16-ounce drink that contains 80 mg of caffeine. Suppose the caffeine in your bloodstream peaks at 80 mg. 1. How much caffeine will remain in your bloodstream after 5 hours? 10 hours? 1 hour? 2 hours? Record your answers in the table

Answer 1

After five hours, there will be 40 mg of caffeine remaining in the blood.

After 10 hours, 20 mg.

After only one hour, about 69.64 mg.

And after two hours, about 60.63 mg.

Explanation:

We are given that one-half of the caffeine in the bloodstream is eliminated every five hours.

We are also given that the initial amount is 80 mg.

Using this information, we can write the following function:

`\displaystyle f(x)=80\left((1)/(2)\right)^{(x)/(5) }`

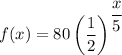
Where x is the number of hours that has passed.

Using this function, we can evaluate for f(5), f(10), f(1), and f(2).

They evaluate to:

`f(5)=40`
`f(10)=20`
`f(1)\approx 69.6440`
`f(2) \approx 60.6287`

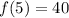
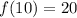
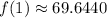
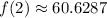
So, after five hours, there are 40 mg of caffeine remaining in the blood.

After 10 hours, 20 mg of caffeine.

After only one hour, about 69.64 mg.

And after two hours, about 60.63 mg.