Answer:
C.) The standard deviation of Data Set 1 is about twice the standard deviation of Data Set 2.
Explanation:
- Data Set 1: 1,2,3,3,6
- Data Set 2: 2,2,3,3,4,4
Data Set 1

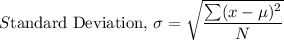
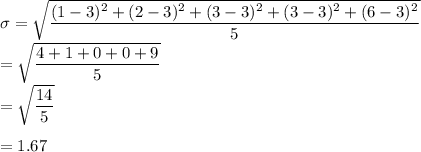
Data Set 2
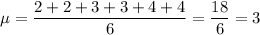

0.89 X 2=1.78 which is close to 1.67
Therefore, the standard deviation of Data Set 1 is about twice the standard deviation of Data Set 2.