Question

The television show 50 Minutes has been successful for many years. That show recently had a share of 20, meaning that among the TV sets in use, 20% were tuned to 50 Minutes. Assume that an advertiser wants to verify that 20% share value by conducting its own survey, and a pilot survey begins with 14 households have TV sets in use at the time of a 50 Minutes broadcast. Find the probability that none of the households are tuned to 50 Minutes.

Answer 1

The probability that none of the households are tuned to 50 Minutes is 0.04398.

Explanation:

We are given that the television show 50 Minutes has been successful for many years. That show recently had a share of 20, meaning that among the TV sets in use, 20% were tuned to 50 Minutes.

A pilot survey begins with 14 households have TV sets in use at the time of a 50 Minutes broadcast.

The above situation can be represented through binomial distribution;

`P(X = r)= \binom{n}{r} * p^(r) * (1-p)^(n-r) ;x = 0,1,2,3,.........`

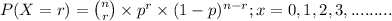
where, n = number of samples (trials) taken = 14 households

r = number of success = none of the households are tuned to 50 min

p = probability of success which in our question is probability that households were tuned to 50 Minutes, i.e. p = 20%

Let X = Number of households that are tuned to 50 Minutes

So, X ~ Binom(n = 14, p = 0.20)

Now, the probability that none of the households are tuned to 50 Minutes is given by = P(X = 0)

P(X = 0) =
`\binom{14}{0} * 0.20^(0) * (1-0.20)^(14-0)`

=
`1 * 1 * 0.80^(14)`

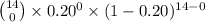
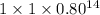
= 0.04398