Question

A fisherman notices that his boat is moving up and down periodically, owing to waves on the surface of the water. It takes 3.5 s for the boat to travel from its highest point to its lowest, a total distance of 0.69 m. The fisherman sees that the wave crests are spaced 6.6 m apart. Part A How fast are the waves traveling

Answer 1

v= 0.94 m/s

Step-by-step explanation:

In order to calculate the speed of the waves, you use the following formula for the speed of the waves:

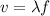`v=\lambda f` (1)

v: speed of the wave

λ: wavelength of the wave

f: frequency of the wave

The frequency is calculated by using the information about the time that boat takes to travel from its highest point to its lowest point. This time is a half of a period:

`(T)/(2)=3.5s\\\\T=7.0s`

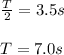
Then, the frequency is:

`f=(1)/(T)=(1)/(7s)=0.142Hz`

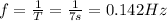
The wavelength of the wave is the distance between crests of the wave

`\lambda=6.6m`

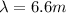
With the values of the frequency and the wavelength, you can find the speed of the wave by using the equation (1):

`v=(6.6m)(0.142Hz)=0.94(m)/(s)`

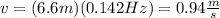
The speed of the wave is 0.94m/s