Answer:
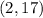
Explanation:
A parabola has the general function:
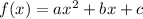
In this case we have:
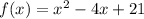
where
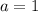
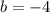
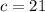
the vertex of a parabola is in the coordinates:
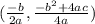
substituting all of the known values, we get the following:
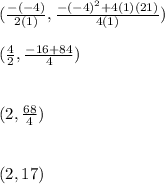
the vertex of
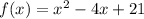 is at the point (2,17) which is the second option.
is at the point (2,17) which is the second option.