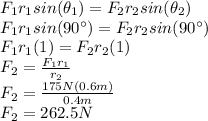Question

Two children push on opposite sides of a door during play. Both push horizontally and perpendicular to the door. One child pushes with a force of 175 N at a distance of 0.600 m from the hinges, and the second pushes at a distance of 0.400 m. What force (in N) must the second exert to keep the door from moving? Assume friction is negligible.

Answer 1

`F_2=\262.5N`

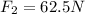
Step-by-step explanation:

Since we need to find the force that the second child must exert to keep the door from moving, that means that the door is in equilibrium, which occurs when the net torque is zero:

`\sum \tau=0\\\tau_1-\tau_2=0(1)`

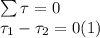
The torque is defined as:

`\tau=Frsin\theta`

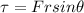
Where F is the applied force, r is the distance between the force and the pivot point (hinges) and
`\theta` is the angle between F and r. Both children push perpendicular to the door, so we have
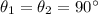`\theta_1=\theta_2=90^\circ`. Replacing in (1) and solving for
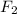`F_2`:

`F_1r_1sin(\theta_1)=F_2r_2sin(\theta_2)\\F_1r_1sin(90^\circ)=F_2r_2sin(90^\circ)\\F_1r_1(1)=F_2r_2(1)\\F_2=(F_1r_1)/(r_2)\\F_2=(175N(0.6m))/(0.4m)\\F_2=262.5N`