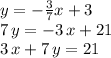Answer:
The equation of the line in slope-intercept form is:
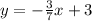
In one of the many possible standard forms:
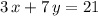
Explanation:
First calculate the slope of the segment that joins these two points: (0, 3) and (7,0):
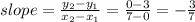
Now, knowing that the y-intercept is (0, 3) [point on the y-axis (for x=0) where the line crosses], Then the equation of the line in slope-intercept form is:
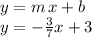
And now, if you want to write the equation eliminating fractions, we can multiply both sides by "7":