Question

Water flowing through a cylindrical pipe suddenly comes to a section of pipe where the diameter decreases to 86% of its previous value. If the speed of the water in the larger section of the pipe was what is its speed in this smaller section if the water behaves like an ideal incompressible fluid

Answer 1

Step-by-step explanation:

The speed of the water in the large section of the pipe is not stated

so i will assume 36m/s

(if its not the said speed, input the figure of your speed and you get it right)

Continuity equation is applicable for ideal, incompressible liquids

Q the flux of water that is Av with A the cross section area and v the velocity,

so,

`A_1V_1=A_2V_2`

`A_(1)=(\pi)/(4)d_(1)^(2) \\\\ A_(2)=(\pi)/(4)d_(2)^(2)`

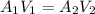
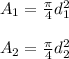
the diameter decreases 86% so

`d_2 = 0.86d_1`

`v_(2)=((\pi)/(4)d_(1)^(2)v_(1))/((\pi)/(4)d_(2)^(2))\\\\=\frac{\cancel{(\pi)/(4)d_(1)^(2)}v_(1)}{\cancel{(\pi)/(4)}(0.86\cancel{d_(1)})^(2)}\\\\\approx1.35v_(1) \\\\v_(2)\approx(1.35)(38)\\\\\approx48.6\,(m)/(s)`

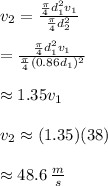
Thus, speed in smaller section is 48.6 m/s