Question

A reheat Rankine cycle operates with water as the working fluid. Steam enters the first turbine at 8 MPa and 450°C and exits at 0.8 MPa. It is then reheated to 400°C before entering the second turbine, where it exits at 10 kPa. If the amount of work into the pump is 8.04 kJ/kg and the net work per cycle produced is 1410.25 kJ/kg, determine the thermal efficiency of the cycle

Answer 1

The thermal efficiency,
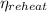`\eta _(reheat)`, of the Rankine cycle with reheat is 36.81%

Step-by-step explanation:

p₁ = 8 MPa = 80 Bars

T₁ = 450°C = 723.15 K

From steam tables, we have;

v₁ = 0.0381970 m³/kg

h₁ = 3273.23 kJ/kg

s₁ = 6.5577 kJ/(kg·K) = s₂

The p₂ = 0.8 MPa

T₂ = Saturation temperature at 0.8 MPa = 170.414°C = 443.564 K

h₂ = 2768.30 kJ/kg

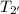`T_(2')` = 400°C = 673.15 K

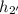`h_(2')` = at 400°C and 0.8 MPa = 3480.6 kJ/kg

p₃ = 10 kPa = 0.1 Bar

T₃ = Saturation temperature at 10 kPa = 45.805 °C = 318.955 K

h₃ = 2583.89 kJ/kg

h₄ =
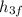`h_(3f)` = 191.812 kJ/kg

The thermal efficiency,
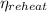`\eta _(reheat)`, of a Rankine cycle with reheat is given as follows;

`\eta _(reheat) = (\left (h_(1)-h_(2) \right )+\left (h_(2')-h_(3) \right )-W_(p))/(h_(1)-\left (h_(4)+W_(p) \right )+\left (h_(2')-h_(2) \right ))`

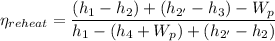
Therefore, we have;

`\eta _(reheat) = ((3273.23 -2768.30 ) + (3480.6 -2583.89 ) - 8.04))/((3273.23 -(191.812 + 8.04) + (3480.6 -2768.30 ) ) = 0.3681`

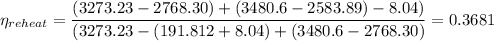
Which in percentage is 36.81%.