Question

when their center-to-center separation is 50 cm. The spheres are then connected by a thin conducting wire. When the wire is removed, the spheres repel each other with an electrostatic force of 0.2525 N. What were the initial charges on the spheres

Answer 1

q1 = 7.6uC , -2.3 uC

q2 = 7.6uC , -2.3 uC

( q1 , q2 ) = ( 7.6 uC , -2.3 uC ) OR ( -2.3 uC , 7.6 uC )

Step-by-step explanation:

Solution:-

- We have two stationary identical conducting spheres with initial charges ( q1 and q2 ). Such that the force of attraction between them was F = 0.6286 N.

- To model the electrostatic force ( F ) between two stationary charged objects we can apply the Coulomb's Law, which states:

`F = k(|q_1|.|q_2|)/(r^2)`

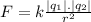
Where,

k: The coulomb's constant = 8.99*10^9

- Coulomb's law assume the objects as point charges with separation or ( r ) from center to center.

- We can apply the assumption and approximate the spheres as point charges under the basis that charge is uniformly distributed over and inside the sphere.

- Therefore, the force of attraction between the spheres would be:

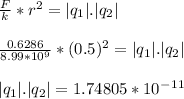`(F)/(k)*r^2 =| q_1|.|q_2| \\\\(0.6286)/(8.99*10^9)*(0.5)^2 = | q_1|.|q_2| \\\\ | q_1|.|q_2| = 1.74805 * 10^-^1^1` ... Eq 1

- Once, we connect the two spheres with a conducting wire the charges redistribute themselves until the charges on both sphere are equal ( q' ). This is the point when the re-distribution is complete ( current stops in the wire).

- We will apply the principle of conservation of charges. As charge is neither destroyed nor created. Therefore,

`q' + q' = q_1 + q_2\\\\q' = (q_1 + q_2)/(2)`

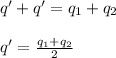
- Once the conducting wire is connected. The spheres at the same distance of ( r = 0.5m) repel one another. We will again apply the Coulombs Law as follows for the force of repulsion (F = 0.2525 N ) as follows:

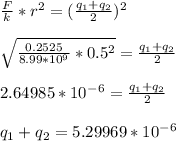`(F)/(k)*r^2 = ((q_1 + q_2)/(2))^2\\\\\sqrt{(0.2525)/(8.99*10^9)*0.5^2} = (q_1 + q_2)/(2)\\\\2.64985*10^-^6 = (q_1 + q_2)/(2)\\\\q_1 + q_2 = 5.29969*10^-^6` .. Eq2

- We have two equations with two unknowns. We can solve them simultaneously to solve for initial charges ( q1 and q2 ) as follows:

`-(1.74805*10^-^1^1)/(q_2) + q_2 = 5.29969*10^-^6 \\\\q^2_2 - (5.29969*10^-^6)q_2 - 1.74805*10^-^1^1 = 0\\\\q_2 = 0.0000075998, -0.000002300123`

`q_1 = -(1.74805*10^-^1^1)/(-0.0000075998) = -2.3001uC\\\\q_1 = (1.74805*10^-^1^1)/(0.000002300123) = 7.59982uC\\`