Question

A wire with mass 90.0 g is stretched so that its ends are tied down at points 98.0 cm apart. The wire vibrates in its fundamental mode with frequency 60.0 Hz and with an amplitude of 0.300 cm at the antinodes. Part A What is the speed of propagation of transverse waves in the wire

Answer 1

118 m/s

Step-by-step explanation:

Given :

We know that

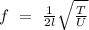`f\ =\ (1)/(2l) \sqrt{(T)/(U) }`......Eq(1)

Where
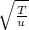`\sqrt{(T)/(u) }` =v

l=length

f=frequency

l= 98.0 cm= 0.98 m

f=60.0 Hz

Now from the Eq(1)

`f\ =\ (v)/(2l)`

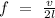
This equation can be written as

v=2fl.............Eq(2)

Putting the value f and l in Eq(2)

v=2*60*0.98

v=117.6 m/s ~ 118 m/s