Question

The final exam grade of a mathematics class has a normal distribution with mean of 81 and standard deviation of 6.6. If a random sample of 40 students selected from this class, then what is the probability that the average final exam grade of this sample is between 77 and 82? Answer: (round to 4 decimal places)

Answer 1

The probability that the average final exam grade of this sample is between 77 and 82

P(77≤ x⁻≤ 82 = 0.8315 or 83%

Explanation:

Step(i):-

Given random sample size 'n' = 40

Mean of the normal distribution = 81

Standard deviation of normal distribution = 6.6

Let x₁⁻ = 77

`Z_(1) = (x_(1) -mean )/((S.D)/(√(n) ) ) = (77-81)/((6.6)/(√(40) ) )`

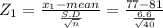
Z₁ = -3.83

Let x₂⁻ = 77

`Z_(2) = (x^(-) _(2) -mean )/((S.D)/(√(n) ) ) = (82-81)/((6.6)/(√(40) ) )`

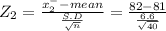
Z₂ = 0.958

The probability that the average final exam grade of this sample is between 77 and 82

P(77≤ x≤ 82) = P( -3.83 ≤x≤0.958)

= A( 0.958) + A(3.83)

= 0.3315 + 0.4995

= 0.8315

The probability that the average final exam grade of this sample is between 77 and 82 = 0.8315 or 83%