Answer:
The expected value of this game is -$0.26.
Explanation:
Expected value:
Each possible earning/loss multiplied by it's probability.
Probability:
Number of desired outcomes divided by the number of total outcomes.
In this question, the order in which the numbers are chosen is not important. So we use the combinations formula to solve.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

Probability of winning:
Desired outcomes:
The 6 correct numbers, so
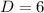
Total outcomes:
6 numbers from a set of 21. So
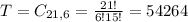
Probability:
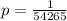
Expected value
 probability of earning 40,000.
probability of earning 40,000.
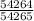 probability of losing 1. So
probability of losing 1. So
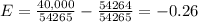
The expected value of this game is -$0.26.