Question

Many companies use well-known celebrities as spokespersons in their TV advertisements. A study was conducted to determine whether brand awareness of TV viewers and the gender of the spokesperson are independent. Each in a sample of 300 TV viewers was asked to identify a product advertised by a celebrity spokesperson. The gender of the spokesperson and whether or not the viewer could identify the product was recorded. The numbers in each category are given below. Find the rejection region necessary for testing at the 0.05 level of significance whether there is a relationship between brand awareness of TV viewers and the gender of the spokesperson.

Answer 1

There is enough evidence to support the claim that the proportion of brand awareness of female TV viewers and the gender of the spokesperson are not independent (P-value = 0.01537).

Explanation:

The question is incomplete: the picture attached gives the missing sample data.

This is a hypothesis test for the difference between proportions.

The claim that is going to be stated in the alternative hypothesis is that the proportion of brand awareness of female TV viewers and the gender of the spokesperson are not independent. This means that the proportions differ significantly.

Then, the null and alternative hypothesis can be written as:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2\\eq 0`

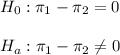
The significance level is 0.05.

The sample 1 (Male celebrity), of size n1=150 has a proportion of p1=0.273.

`p_1=X_1/n_1=41/150=0.273`

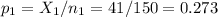
The sample 2 (Female celebrity), of size n2=150 has a proportion of p2=0.407.

`p_2=X_2/n_2=61/150=0.407`

The difference between proportions is (p1-p2)=-0.133.

`p_d=p_1-p_2=0.273-0.407=-0.133`

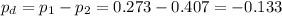
The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(41+61.05)/(150+150)=(102)/(300)=0.34`

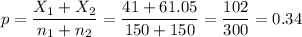
The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.34*0.66)/(150)+(0.34*0.66)/(150)}\\\\\\s_(p1-p2)=√(0.001496+0.001496)=√(0.002992)=0.055`

Then, we can calculate the z-statistic as:

`z=(p_d-(\pi_1-\pi_2))/(s_(p1-p2))=(-0.133-0)/(0.055)=(-0.133)/(0.055)=-2.44`

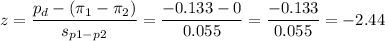
This test is a two-tailed test, so the P-value for this test is calculated as (using a z-table):

`P-value=2\cdot P(z<-2.44)=0.01537`

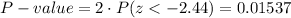
As the P-value (0.01537) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the proportion of brand awareness of female TV viewers and the gender of the spokesperson are not independent (the proportions differ).