Question

A poll surveyed 503 video gamers, and 106 of them said they prefer playing games on a console rather than a computer. An executive at a game console company claims that more than 25% of gamers prefer consoles. Does the poll provide convincing evidence that the claim is true? Use the level of significance.

Answer 1

The claim has no evidence to be supported.

On the contrary, there is enough evidence to support the claim that less than 25% of gamers prefer consoles.

Explanation:

This is a hypothesis test for a proportion.

The sample has a size n=503.

The sample proportion is p=0.211.

p=X/n=106/503=0.211

The sample proportion is less than 25%, so we will test the claim that less than 25% of gamers prefer consoles.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.25\\\\H_a:\pi<0.25`

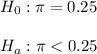
The significance level is assumed to be 0.05.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.25*0.75)/(503)}\\\\\\ \sigma_p=√(0.000373)=0.019`

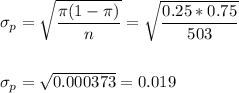
Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/n)/(\sigma_p)=(0.211-0.25+0.5/503)/(0.019)=(-0.038)/(0.019)=-1.9685`

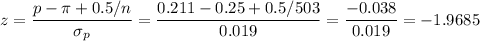
This test is a left-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z<-1.9685)=0.0245`

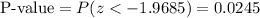
As the P-value (0.0245) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that less than 25% of gamers prefer consoles.