Answer:
They are right, the time calculated using the exponential decay equation is 1948.6 years.
Explanation:
The time can be calculated using the exponential decay equation:
 (1)
(1)
Where:
N(t): is the quantity of C-14 at time t
N₀: is the initial quantity of C-14
λ: is the decay constant
The decay constant is:
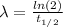 (2)
(2)
By entering equation (2) into (1) and solving for t, we have:
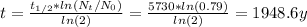
Therefore, the time of the scrolls estimated by the archeologists is right, since the time calculated using the exponential decay equation is 1948.6 years.
I hope it helps you!