Question

At some instant and location, the electric field associated with an electromagnetic wave in vacuum has the strength 65.9 V/m. Find the magnetic field strength B, the total energy density u, and the power flow per unit area, all at the same instant and location.

Answer 1

B = 2.19*10^-7 T

u = 1.92*10^-18 J/m^3

P = (4pi r^2)cεo E^2

Step-by-step explanation:

In order to find the magnetic field strength of the electromagnetic wave you use the following formula:

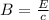`B=(E)/(c)` (1)

B: magnitude of the magnetic field

E: magnitude of the electric field = 65.9V/m

c: speed of light = 3*10^8m/s

`B=(65.9V/m)/(3*10^8m/s)=2.19*10^(-7)T`

The magnitude of the magnetic field 2.19*10^-7 T

The energy density of the electromagnetic wave is:

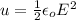`u=(1)/(2)\epsilon_oE^2` (2)

εo: dielectric permittivity = 8.85*10^-12C^2/Nm^2

`u=(1)/(2)(8.85*10^(-12)C^2/Nm^2)(65.9V/m)^2=1.92*10^(-8)(J)/(m^3)`

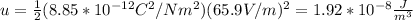
The energy density of the electromagnetic wave is 1.92*10^-8J/m^3

The power is given by:

`P=IA=c\epsilon_oE^2(4\pi r^2)`