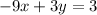Question

Find the value of $B - A$ if the graph of $Ax + By = 3$ passes through the point $(-7,2),$ and is parallel to the graph of $x + 3y = -5.$

Answer 1

Since B is equal to -9, then A must be equal to 3. "B - A" is equal to -12 The expression of the line is then:
`-9x + 3y = 3`

Explanation:

In order to solve this problem, lets first find the slope of the line. Since the line we want to know is parallel to "x + 3y = -5", then their slopes are the same, therefore:

`x + 3y = -5\\3y = -5 -x\\y = -(x)/(3) - (5)/(3)`

The slope of the line is the number that multiplies "x", therefore m =
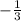`-(1)/(3)`. Organizing the first equation to the form we need, gives us:

`Ax + By = 3\\By = 3 - Ax\\y = -(A)/(B)x + (3)/(B)`

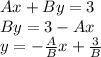
We know that
`-(A)/(B) = -(1)/(3)` because the lines are parallel, if we apply the point given we will find the value of B and therefore the value of A.

`y = -(1)/(3)x + (3)/(B)\\2 = -(1)/(3)*(-7) + (3)/(B)\\2 = (7)/(3) + (3)/(B)\\(3)/(B) = 2 - (7)/(3)\\(3)/(B) = (6 - 7)/(3)\\(3)/(B) = (-1)/(3)\\B = -9`

`B - A = -9 -3 = -12`

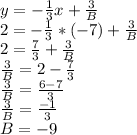
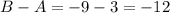
Since B is equal to -9, then A must be equal to 3. "B - A" is equal to -12. The expression of the line is then:
`-9x + 3y = 3`