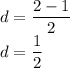Question

I have two questions. Please try to answer both!

How many non-similar triangles have angles whose degree measures are distinct positive integers in an arithmetic progression?


In an arithmetic sequence a7 −2a4 = 1, a3 = 0. Find the common difference.


Thank you!

Answer 1

(a)59

(b)
`d=(1)/(2)`

Explanation:

Part A

The nth term of an arithmetic sequence,
`T_n=a+(n-1)d`

Let the first angle of the triangle =a

Let the common difference = d.

Since the measures of the angles are in an arithmetic progression

We have:

a + (a + d) + (a + 2d) = 180

3a+3d=180

a+d=60

Since a or d cannot be equal to zero, the minimum possible values of a and d is 1 and the maximum possible values of a and d is 59.

Therefore, there are 59 non-similar triangles.

Part B

In an arithmetic sequence

`a_7 -2a_4 = 1, a_3 = 0.`

`2a_4=a_7-1\\a_4=(a_7-1)/(2)`

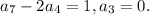
Common difference,

`d=a_4-a_3\\=(a_7-1)/(2)-0\\d=(a_7-1)/(2)`

`a_7=a_4+3d\\=(a_7-1)/(2)+3((a_7-1)/(2))\\=(a_7-1)/(2)+(3a_7-3)/(2)\\=(a_7-1+3a_7-3)/(2)\\a_7=(4a_7-4)/(2)\\$Cross multiply\\2a_7=4a_7-4\\2a_7-4a_7=-4\\-2a_7=-4\\a_7=2`

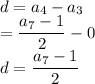
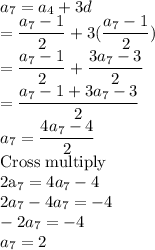
Therefore:

`d=(2-1)/(2)\\d=(1)/(2)`