Question

A company plans to manufacture a rectangular bin with a square base, an open top, and a volume of 13,500 in3. Determine the dimensions of the bin that will minimize the surface area. What is the minimum surface area

Answer 1

Dimensions 30 in x 30 in x 15 in

Surface Area = 2,700 in²

Explanation:

Let 'r' be the length of the side of the square base, and 'h' be the height of the bin. The volume is given by:

`V=13,500=h*r^2\\h=(13,500)/(r^2)`

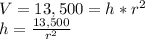
The total surface area is given by:

`A=4*hr+r^2`

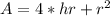
Rewriting the surface area function as a function of 'r':

`A=4*(13,500)/(r^2) *r+r^2\\A=(54,000)/(r)+r^2`

The value of 'r' for which the derivate of the surface area function is zero, is the length for which the area is minimized:

`A=54,000*r^(-1)+r^2\\(dA)/(dr)=0= -54,000*r^(-2)+2r\\(54,000)/(r^2)=2r\\ r=\sqrt[3]{27,000}\\r=30\ in`

The value of 'h' is:

`h=(13,500)/(30^2)\\ h=15\ in`

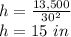
The dimensions that will ensure the minimum surface area are 30 in x 30 in x 15 in.

The surface area is:

`A=4*15*30+30^2\\A=2,700\ in^2`