Question

A rectangular box with a volume of 684 ftcubed is to be constructed with a square base and top. The cost per square foot for the bottom is 20cents​, for the top is 15cents​, and for the sides is 1.5cents. What dimensions will minimize the​ cost?

Answer 1

The dimensions of the rectangular box is 36.23 ft×36.23 ft×4.345 ft.

Minimum cost=2046.16 cents

Explanation:

Given that a rectangular box with a volume of 684 ft³.

The base and the top of the rectangular box is square in shape

Let the length and width of the rectangular box be x.

[since the base is square in shape, length=width]

and the height of the rectangular box be h.

The volume of rectangular box is = Length ×width × height

=(x²h) ft³

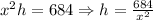`x^2h=684\Rightarrow h=(684)/(x^2)` (1)

The area of the base and top of rectangular box is = x² ft²

The surface area of the sides= 2(length+width) height

=2(x+x)h

=4xh ft²

The total cost to construct the rectangular box is

=[(x²×20)+(x²×15)+(4xh×1.5)] cents

=(20x²+15x²+6xh) cents

=(25x²+6xh) cents

Total cost= C(x).

C(x) is in cents.

∴C(x)=25x²+6xh

Putting
`h=(684)/(x^2)`

`C(x)=25x^2+6x*(684)/(x^2) \Rightarrow C(x)=25x^2+(4104)/(x)`

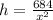
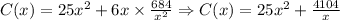
Differentiating with respect to x

`C'(x)=50x-(4104)/(x^2)`

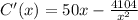
To find minimum cost, we set C'(x)=0

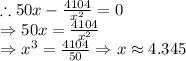`\therefore50x-(4104)/(x^2)=0\\\Rightarrow50x=(4104)/(x^2)\\\Rightarrow x^3=(4104)/(50)\Rightarrow x\approx 4.345` ft.

Putting the value x in equation (1) we get

`h=(684)/((4.345)^2)`

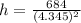
≈36.23 ft.

The dimensions of the rectangular box is 36.23 ft×36.23 ft×4.345 ft.

Minimum cost C(x)=[25(4.345)²+10(4.345)(36.23)] cents

=2046.16 cents