Question

An oscillator consists of a block of mass 0.373 kg connected to a spring. When set into oscillation with amplitude 33 cm, the oscillator repeats its motion every 0.412 s. Find the (a) period, (b) frequency, (c) angular frequency, (d) spring constant, (e) maximum speed, and (f) magnitude of the maximum force on the block from the spring.

Answer 1

(a) T = 0.412s

(b) f = 2.42Hz

(c) w = 15.25 rad/s

(d) k = 86.75N/m

(e) vmax = 5.03 m/s

Step-by-step explanation:

Given information:

m: mass of the block = 0.373kg

A: amplitude of oscillation = 22cm = 0.22m

T: period of oscillation = 0.412s

(a) The period is the time of one complete oscillation = 0.412s

The period is 0.412s

(b) The frequency is calculated by using the following formula:

`f=(1)/(T)=(1)/(0.412s)=2.42Hz`

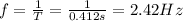
The frequency is 2.42 Hz

(c) The angular frequency is:

`\omega=2\pi f=2\pi (2.42Hz)=15.25(rad)/(s)`

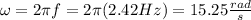
The angular frequency is 15.25 rad/s

(d) The spring constant is calculated by solving the following equation for k:

`\omega=\sqrt{(k)/(m)}\\\\k=m\omega^2=(0.373kg)(15.25rad/s)^2=86.75(N)/(m)`

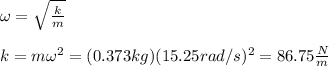
The spring constant is 86.75N/m

(e) The maximum speed is:

`v_(max)=\omega A=(15.25rad/s)(0.33m)=5.03(m)/(s)`

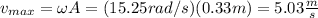
(f) The maximum force applied by the spring if for the maximum elongation, that is, the amplitude:

`F=kA=(86.75N/m)(0.2m)=17.35N`

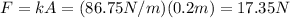
The maximum force that the spring exerts on the block is 17.35N