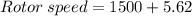Question

A 50 Hz, four pole turbo-generator rated 100 MVA, 11 kV has an inertia constant of 8.0 MJ/MVA. (a) Find the stored energy in the rotor at synchronous speed. (b) If the mechanical input is suddenly raised to 80 MW for an electrical load of 50 MW, find rotor acceleration, neglecting mechanical and electrical losses. (c) If the acceleration calculated in part(b) is maintained for 10 cycles, find the change in torque angle and rotor speed in revolutions per minute at the end of this period.

Answer 1

Given Information:

Frequency = f = 60 Hz

Complex rated power = G = 100 MVA

Intertia constant = H = 8 MJ/MVA

Mechanical power = Pmech = 80 MW

Electrical power = Pelec = 50 MW

Number of poles = P = 4

No. of cycles = 10

Required Information:

(a) stored energy = ?

(b) rotor acceleration = ?

(c) change in torque angle = ?

(c) rotor speed = ?

Answer:

(a) stored energy = 800 Mj

(b) rotor acceleration = 337.46 elec deg/s²

(c) change in torque angle (in elec deg) = 6.75 elec deg

(c) change in torque angle (in rmp/s) = 28.12 rpm/s

(c) rotor speed = 1505.62 rpm

Step-by-step explanation:

(a) Find the stored energy in the rotor at synchronous speed.

The stored energy is given by

`E = G * H`

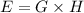
Where G represents complex rated power and H is the inertia constant of turbo-generator.

`E = 100 * 8 \\\\E = 800 \: MJ`

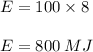
(b) If the mechanical input is suddenly raised to 80 MW for an electrical load of 50 MW, find rotor acceleration, neglecting mechanical and electrical losses.

The rotor acceleration is given by

`$ P_a = P_(mech) - P_(elec) = M (d^2 \delta)/(dt^2) $`

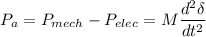
Where M is given by

`$ M = (E)/(180 * f) $`

`$ M = (800)/(180 * 50) $`

`M = 0.0889 \: MJ \cdot s/ elec \: \: deg`

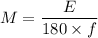
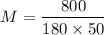
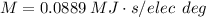
So, the rotor acceleration is

`$ P_a = 80 - 50 = 0.0889 (d^2 \delta)/(dt^2) $`

`$ 30 = 0.0889 (d^2 \delta)/(dt^2) $`

`$ (d^2 \delta)/(dt^2) = (30)/(0.0889) $`

`$ (d^2 \delta)/(dt^2) = 337.46 \:\: elec \: deg/s^2 $`

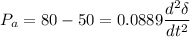
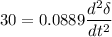
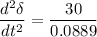
(c) If the acceleration calculated in part(b) is maintained for 10 cycles, find the change in torque angle and rotor speed in revolutions per minute at the end of this period.

The change in torque angle is given by

`$ \Delta \delta = (1)/(2) \cdot (d^2 \delta)/(dt^2)\cdot (t)^2 $`

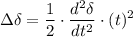
Where t is given by

`1 \: cycle = 1/f = 1/50 \\\\10 \: cycles = 10/50 = 0.2 \\\\t = 0.2 \: sec`

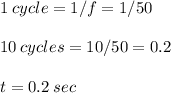
So,

`$ \Delta \delta = (1)/(2) \cdot 337.46 \cdot (0.2)^2 $`

`$ \Delta \delta = 6.75 \: elec \: deg`

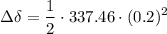
The change in torque in rpm/s is given by

`$ \Delta \delta = (337.46 \cdot 60)/(2 \cdot 360\circ ) $`

`$ \Delta \delta =28.12 \: \: rpm/s $`

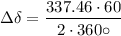
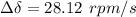
The rotor speed in revolutions per minute at the end of this period (10 cycles) is given by

`$ Rotor \: speed = (120 \cdot f)/(P) + (\Delta \delta)\cdot t $`

Where P is the number of poles of the turbo-generator.

`$ Rotor \: speed = (120 \cdot 50)/(4) + (28.12)\cdot 0.2 $`

`$ Rotor \: speed = 1500 + 5.62 $`

`$ Rotor \: speed = 1505.62 \:\: rpm`