Question

X is a normally distributed random variable with the standard deviation of 4.00.Find the mean of X when 64.8%

Answer 1

μ = 9.504

Explanation:

I get complete question that is x is a normally distributed random variable with a standard deviation of 4.00. find the mean of x when 64.8% of the area lies to the left of 11.02

given data

standard deviation = 4

solution

we know that that

X ∞ Normal ( μ , 4²) ...............1

so Probability P will be express as

P ( X < 11.02 ) = 64.8%

so here

P ( Z <
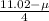`(11.02- \mu )/(4)` ) = 0.648

Z for 0.648 =
`(11.02- \mu )/(4)`

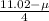
0.379 =
`(11.02- \mu )/(4)`

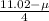
solve it we get

μ = 9.504