Question

two technicians regularly make repairs when breakdowns occur on an automated production line. the first technican, who services 40% of the breakdowns, has 5% chance of making incomplete repair. the second technican, who services 60% of the breakdowns, has 3% chance of making an incomplete repair. given that there is a problem with the production line due to an incomplete repair, what is the probability that thids intial repair was made by the first technican

Answer 1

52.63% probability that thids intial repair was made by the first technican

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

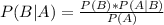
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Incomplete repair

Event B: Made by the first technican.

The first technican, who services 40% of the breakdowns, has 5% chance of making incomplete repair.

This means that
`P(B) = 0.4, P(A|B) = 0.05`.

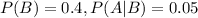Probability of an incomplete repair:

5% of 40%(first technican) or 3% of 60%(second technican). So

`P(A) = 0.05*0.4 + 0.03*0.6 = 0.038`

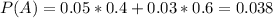
Given that there is a problem with the production line due to an incomplete repair, what is the probability that thids intial repair was made by the first technican

`P(B|A) = (0.4*0.05)/(0.038) = 0.5263`

52.63% probability that thids intial repair was made by the first technican