Answer:
The final specific internal energy of the system is 1509.91 kJ/kg
Step-by-step explanation:
The parameters given are;
Mass of steam = 1 kg
Initial pressure of saturated steam p₁ = 1000 kPa
Initial volume of steam, = V₁
Final volume of steam = 5 × V₁
Where condition of steam = saturated at 1000 kPa
Initial temperature, T₁ = 179.866 °C = 453.016 K
External pressure = Atmospheric = 60 kPa
Thermodynamic process = Adiabatic expansion
The specific heat ratio for steam = 1.33
Therefore, we have;
![(p_1)/(p_2) = \left ((V_2)/(V_1) \right )^k = \left [(T_1)/(T_2) \right ]^{(k)/(k-1)}](https://img.qammunity.org/2021/formulas/engineering/college/defr1buy9lmafxr4ty61anuw84wt1a0oyc.png)
Adding the effect of the atmospheric pressure, we have;
p = 1000 + 60 = 1060
We therefore have;
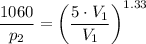
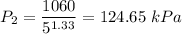
![\left [(V_2)/(V_1) \right ]^k = \left [(T_1)/(T_2) \right ]^{(k)/(k-1)}](https://img.qammunity.org/2021/formulas/engineering/college/n51bacmbw43rvtvqpsh1wa4i9a27juxhlx.png)
![\left [(V_2)/(V_1) \right ]^(k-1) = \left (T_1)/(T_2) \right](https://img.qammunity.org/2021/formulas/engineering/college/471zzkll3l1d43lchopyyqpg2esov0ecgi.png)
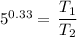
T₁/T₂ = 1.70083
T₁ = 1.70083·T₂
T₂ - T₁ = T₂ - 1.70083·T₂
Whereby the temperature of saturation T₁ = 179.866 °C = 453.016 K, we have;
T₂ = 453.016/1.70083 = 266.35 K
ΔU = 3×
 ×(T₂ - T₁)
×(T₂ - T₁)
 = cv for steam at 453.016 K = 1.926 + (453.016 -450)/(500-450)*(1.954-1.926) = 1.93 kJ/(kg·K)
= cv for steam at 453.016 K = 1.926 + (453.016 -450)/(500-450)*(1.954-1.926) = 1.93 kJ/(kg·K)
cv for steam at 266.35 K = 1.86 kJ/(kg·K)
We use cv given by (1.93 + 1.86)/2 = 1.895 kJ/(kg·K)
ΔU = 3×
 ×(T₂ - T₁) = 3*1.895 *(266.35 -453.016) = -1061.2 kJ/kg
×(T₂ - T₁) = 3*1.895 *(266.35 -453.016) = -1061.2 kJ/kg
The internal energy for steam =
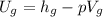
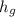 = 2777.12 kJ/kg
= 2777.12 kJ/kg
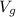 = 0.194349 m³/kg
= 0.194349 m³/kg
p = 1000 kPa
 = 2777.12 - 0.194349 * 1060 = 2571.11 kJ/kg
= 2777.12 - 0.194349 * 1060 = 2571.11 kJ/kg
The final specific internal energy of the system is therefore,
 + ΔU = 2571.11 - 1061.2 = 1509.91 kJ/kg.
+ ΔU = 2571.11 - 1061.2 = 1509.91 kJ/kg.