Answer:
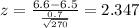
The p value for this case would be given by"
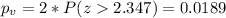
For this case since the p value is higher than the significance level we don't have enough evidence to conclude that the true mean is significantly different from 6.5 lbs/square inch at 10% of significance. So then there is not enough evidence to conclude that the valve does not perform to the specifications
Explanation:
Information given
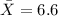 represent the sample mean
represent the sample mean
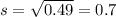 represent the population deviation
represent the population deviation
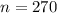 sample size
sample size
 represent the value that we want to test
represent the value that we want to test
 represent the significance level
represent the significance level
z would represent the statistic
 represent the p value for the test
represent the p value for the test
Hypothesis to verify
We want to verify if the true mean for this case is equal to 6.5 lbs/square inch or not , the system of hypothesis would be:
Null hypothesis:
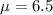
Alternative hypothesis:
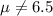
The statistic for this case is given by:
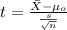 (1)
(1)
And replacing we got:
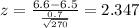
The p value for this case would be given by"
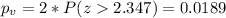
For this case since the p value is higher than the significance level we don't have enough evidence to conclude that the true mean is significantly different from 6.5 lbs/square inch at 10% of significance. So then there is not enough evidence to conclude that the valve does not perform to the specifications