Question

A machine produces a part for the automotive industry. 4% of the parts produced were defective in the past, and we believe that the current percentage is not higher. What is the needed sample size for estimating the current percentage of defective parts with the 90% confidence and the 3% margin of error

Answer 1

`n=(0.04(1-0.04))/(((0.03)/(1.64))^2)=114.76`

And rounded up we have that n=115

Explanation:

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 90% of confidence, our significance level would be given by
`\alpha=1-0.90=0.1` and
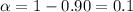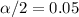`\alpha/2 =0.05`. And the critical value would be given by:

`z_(\alpha/2)=-1.64, z_(1-\alpha/2)=1.64`

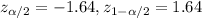
Solution to the problem

The margin of error for the proportion interval is given by this formula:

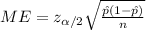`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

The proportion of defectives is estimated as:
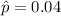`\hat p=0.04`. And on this case we have that the margin of error is
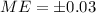`ME =\pm 0.03` and we are interested in order to find the value of n, if we solve n from equation (a) we got:

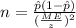`n=(\hat p (1-\hat p))/(((ME)/(z))^2)` (b)

And replacing into equation (b) the values from part a we got:

`n=(0.04(1-0.04))/(((0.03)/(1.64))^2)=114.76`

And rounded up we have that n=115