Question

The numbers of beans in some cocoa pods

are 30, 28, 30, 35, 40, 25, 32, 36, 38 and 40.
a Calculate the mean number of beans per
cocoa pod.
b Calculate the standard deviation of the
distribution.​

Answer 1

a) Mean number of beans = 33.4 per coco pad

b) Standard deviation of the beans = 5.2 per coco pad

Explanation:

Step(i):-

a)

Given data 30, 28, 30, 35, 40, 25, 32, 36, 38 and 40.

mean of beans

x⁻ = ∑x/n

`x^(-) = (30+ 28+30+35+40+25+32+36+38 + 40.)/(10) = 33.4`

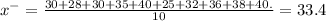
Mean number of beans per coco pad = 33.4

step(ii):-

b)

standard deviation

∑(xi - x⁻)² = (30-33.4)²+ (28-33.4)²+(30-33.4)²+(35-33.4)²+(40-33.4)²+(25-33.4)²+(32-33.4)²+(36-33.4)²+ (38-33.4)²+(40-33.4)²

On calculation , we get

∑(xi - x⁻)² = 242.4

standard deviation

=
`\sqrt{(sum((x-x^(-) )^(2) )/(n-1) } = \sqrt{(242.4)/(10-1) } = 5.189`

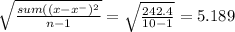
Standard deviation of the beans (σ) = 5.2 per coco pad