Question

g Of 23 fast food restaurants in the city, a total of 5 were in violation of sanitary standards, a total of 6 were in violation of safety standards, and 3 were in violation of both. If a fast food restaurant is chosen at random from these 23, what is the probability that it is in compliance of both safety and sanitary standards?

Answer 1

65.22% probability that it is in compliance of both safety and sanitary standards

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

Number of restaurant in compliance of both safety and sanitary standards.

First I will find those not in compliance, using a Venn's set.

Set A: Violation of sanitary standards.

Set B: Violation of safety standards.

5 were in violation of sanitary standards, a total of 6 were in violation of safety standards, and 3 were in violation of both.

This means that
`A = 5, B = 6, (A \cap B) = 3`

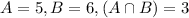
At least one:

`A \cup B = A + B - (A \cap B)`

So

`A \cup B = 5 + 6 - 3 = 8`

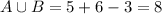
8 are in violation of at least one of these standards.

So 23-8 = 15 are in compliance of both safety and sanitary standards.

What is the probability that it is in compliance of both safety and sanitary standards?

15 out of 23

15/23 = 0.6522

65.22% probability that it is in compliance of both safety and sanitary standards