Question

The number of milligrams of a certain medicine a veterinarian gives to a dog varies directly with the weight of the dog. If the veterinarian gives a 30-pound dog Three-fifths milligram of the medicine, which equation relates the weight, w, and the dosage, d? d = StartFraction 1 Over 50 EndFraction w d = three-fifths w d = 18 w d = 50 w

Answer 1

A

Explanation:

Answer 2

Explanation:

A direct variation equation is of the form

y = kx,

where, in words, it reads "y varies directly with x" or "y varies directly as x". In order to use this as a model, we have to have enough information to solve for k, the constant of variation. The constant of variation is kind of like the slope in a straight line. It rises or falls at a steady level; it is the rate of change.

We have that a vet gives a dose of three-fifths mg to a 30 pound dog. If the dose varies directly with the weight of the dog, then our equation is

d = kw and we need to find k in order to have the model for dosing the animals.

`(3)/(5) =k(30)`

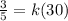
Divide both sides by 1/30 to get k alone.

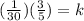`((1)/(30))((3)/(5))=k` and

`k=(1)/(50)`

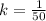
Our model then is

`d=(1)/(50)w`

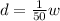
This means that for every pound of weight, the dog will get one-fiftieth of a mg of medicine.