Question

A door of a lecture hall is in a parabolic shape. The door is 56 inches across at the bottom of the door and parallel to the floor and 32 inches high. Sketch and find the equation describing the shape of the door. If you are 22 inches tall, how far must you stand from the edge of the door to keep from hitting your head?

Answer 1

The parabolic shape of the door is represented by
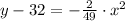`y - 32 = -(2)/(49)\cdot x^(2)`. (See attachment included below). Head must 15.652 inches away from the edge of the door.

Explanation:

A parabola is represented by the following mathematical expression:

`y - k = C \cdot (x-h)^(2)`

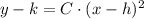
Where:

`h` - Horizontal component of the vertix, measured in inches.

`k` - Vertical component of the vertix, measured in inches.

`C` - Parabola constant, dimensionless. (Where vertix is an absolute maximum when
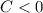`C < 0` or an absolute minimum when
`C > 0`)

For the design of the door, the parabola must have an absolute maximum and x-intercepts must exist. The following information is required after considering symmetry:

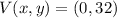`V (x,y) = (0, 32)` (Vertix)

`A (x, y) = (-28, 0)` (x-Intercept)

`B (x,y) = (28. 0)` (x-Intercept)

The following equation are constructed from the definition of a parabola:

`0-32 = C \cdot (28 - 0)^(2)`

`-32 = 784\cdot C`

`C = -(2)/(49)`

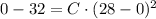
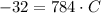
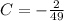
The parabolic shape of the door is represented by
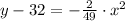`y - 32 = -(2)/(49)\cdot x^(2)`. Now, the representation of the equation is included below as attachment.

At x = 0 inches and y = 22 inches, the distance from the edge of the door that head must observed to avoid being hit is:

`y -32 = -(2)/(49) \cdot x^(2)`

`x^(2) = -(49)/(2)\cdot (y-32)`

`x = \sqrt{-(49)/(2)\cdot (y-32) }`

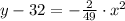
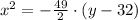
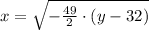
If y = 22 inches, then x is:

`x = \sqrt{-(49)/(2)\cdot (22-32)}`

`x = \pm 7√(5)\,in`

`x \approx \pm 15.652\,in`

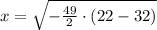
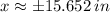
Head must 15.652 inches away from the edge of the door.