Question

TRIGNOMETRY:

Faisal is 30m from a flagpole. The angle of elevation of its top is 12.4° and the angle of depression of the bottom is 2.1°. Find the height of the flagpole, correct to 3 significant figures.

Answer 1

7.698 m

Explanation:

From the question,

Faisal's distance to the flagpole = 30 m

angle of elevation of its top = 12.4°

angle of depression of its bottom = 2.1°

Thus, the height of the flagpole is divided into two parts. Let the upper part be represented by x and the lower part by y.

From the triangle of the upper part (elevation), we have;

tan 12.4° =
`(x)/(30)`

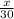
x = 30 × tan 12.4°

= 30 × 0.2199

= 6.597 m

From the triangle of the lower part (depression), we have;

tan 2.1° =
`(y)/(30)`

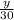
y = 30 × tan 2.1°

= 30 × 0.0367

= 1.101 m

The height of the flagpole = x + y

= 6.597 + 1.101

= 7.698 m

The height of the flagpole is 7.698 m.