Question

A Poker club has 10 members. A president and a vice-president are to be selected. In how many ways can this be done if everyone is eligible?

Answer 1

90 different ways

Explanation:

We have a total of 10 members, and we want to find how many groups of 2 members we can have, where the order of each member in the group of 2 is important, so we have a permutation problem.

To solve this problem, we need to calculate a permutation of 10 choose 2.

The formula for a permutation of n choose p is:

`P(n, p) = n! / (n - p)!`

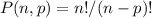
So we have:

`P(10, 2) = 10! / (10 - 2)!`

`P(10, 2) = 10! / 8!`

`P(10, 2) = 10*9 = 90`

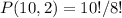
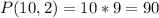
So there are 90 different ways of choosing a president and a vice-president.