Answer:
The answer is A.
Explanation:
First, recall the vertex form of a quadratic equation:
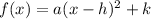 , where
, where
 represents the horizontal change and
represents the horizontal change and
 represents the vertical change.
represents the vertical change.
The original equation is
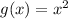 , or, in other words,
, or, in other words,
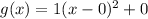 .
.
We are told that the graph is shifted up 3 and right 1. Thus, both values are positive (right and up). Note that up 3 corresponds to a positive vertical change of 3 while right 1 represents a positive horizontal change of 1.
Thus, put these back into the equation in place of
 and
and
 .
.
We have:
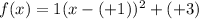
Or, simplified:

The answer is A.