Question

O perímetro de um campo retangular é de 80 metros e sua area é de 320 metros quadrados. Encontre as dimensões do campo, corrija o décimo de metro mais próximo.

Answer 1

Comprimento: 28.9 m; Largura: 11.1 m

Explanation:

P = 2(C + L) = 80

A = CL = 320

2(C + L) = 80

CL = 320

C + L = 40

CL = 320

C = 40 - L

CL = 320

(40 - L)L = 320

40L - L^2 = 320

L^2 - 40L + 320 = 0

aL^2 + bL + c = 0

`L = (-b \pm √(b^2 - 4ac))/(2a)`

`L = (-(40) \pm √((-40)^2 - 4(1)(320)))/(2(1))`

`L = (40 \pm √(1600 - 1280))/(2)`

`L = (40 \pm √(320))/(2)`

`L = (40 \pm √(64 * 5))/(2)`

`L = (40 \pm 8√(5))/(2)`

`L = 20 \pm 4√(5)`

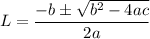
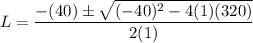
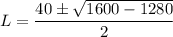
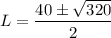
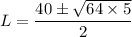
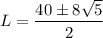
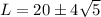
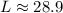`L \approx 28.9` or
`L \approx 11.1`

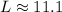
L = 28.9

C = 40 - L = 40 - 28.9 = 11.1

Answer: Comprimento: 28.9 m; Largura: 11.1 m