Question

A water balloon is tossed vertically from a window at an initial height (s-sub zero) of 37 feet and with an initial velocity(v-subzero) of 41 feet per second. Answer the following using the fact that h(t)=-16T^2+v-sub zer0t+s sub zero. a) Determine a formula, h)t), for the function that models the height of the water balloon at time t . b)Plot the function in Desmos in an appropriate window. Use the graph to estimate the time the water balloon lands c)Use algebra to find the exact time the water balloon lands. Show your work. No decimals in your answer. d)Determine the exact time the water balloon reaches its highest point and its height at that time. e)4 pts] Compute the average rate of change of on the intervals . Include units on your answers and write a sentence to explain the meaning of the values you found. Arc{1.5,2}____________________________. Explanation: Arc{2,2.5}____________________________. Explanation: årc{2.5,3}____________________________. Explanation:

Answer 1

(a) h(t) = -16t² + 41t + 37

(b) About 3.3 s

`\large \boxed{\text{(c) }(41+ √(4049))/(32)\text{ s}}`

(d) -15 ft/s; -31 ft/s; -47 ft/s

Explanation:

(a) The function

h(t) = -16t² + v₀t + s₀

v₀ = 41 ft·s⁻¹

s₀ = 37 ft

The function is

h(t) = -16t² + 41t + 37

(b) The graph

See Fig. 1.

It looks like the water balloon lands after about 3.3 s.

(c) Time of landing

h = -16t² + 41t + 37

a = -16; b = 41; c = 37

We can use the quadratic formula to solve the equation:

`h = (-b\pm√(b^2 - 4ac))/(2a) = (-b\pm√(D))/(2a)`

(i) Evaluate the discriminant D

D = b² - 4ac = 41² - 4(-16) × 37 = 1681 + 2368 = 4049

(ii) Solve for t

`\begin{array}{rcl}h& = & (-b\pm√(D))/(2a)\\\\ & = & (-41\pm√(4049))/(2(-16))\\\\ & = & (41\pm√(4049))/(32)\\\\t = (41- √(4049))/(32)&\qquad& t = (41+ √(4049))/(32)\\\\\end{array}\\`

`\text{The water balloon will land after $\large \boxed{\mathbf{(41+ √(4049))/(32)}\textbf{ s}} $}`

(d) Time and maximum height

(i) Time

The axis of symmetry (time of maximum height) is at t = -b/(2a)

`t = (-41)/(2(-16)) = (41)/(32) = \textbf{1.281 s}`

(ii) Maximum height

The vertex is at y = h(1.281) = h(t) = -16(1.281)² + 41(1.281) + 37 = 63.27 ft

(e) Average rate of change

(i) Arc{1.5,2}

h(1.5) = 62.5

h(2) = 55

m = (h₂ - h₁)/(t₂ - t₁) = (55 - 62.5)/(2 - 1.5) = -7.5/0.5 = -15 ft/s

The water balloon has started to fall after it has reached peak height, so it is not going very fast

(ii) Arc{2,2.5}

h(2.5) =39.5

m = (39.5 - 55)/(2 - 1.5) = -15.5/0.5 = -31 ft/s

The balloon is in mid-fall, so gravity has caused it to speed up.

(iii) Arc{2.5,3}

h(3) = 16

m = (16 - 39.5)/(2 - 1.5) = -23.5/0.5 = -47 ft/s

The balloon is about to hit the ground, so it is falling at almost its maximum velocity.

Fig. 2 shows the height of the balloon at the above times.

Answer 2

a) h(t) = -16t^2 +41t +37

b) see attached (3.270 seconds)

c) (41+√4049)/32 seconds

d) 1.28125 seconds; 63.265625 feet

e) [1.5, 2]: -15; [2, 2.5]: -31; [2.5, 3]: -47

Explanation:

a) The formula and initial values are given. Putting those values into the formula, we get ...

h(t) = -16t^2 +41t +37

__

b) The graph is attached. It shows the t-intercept to be about 3.270 seconds.

__

c) Using the quadratic formula, we can find the landing time as ...

`t=(-b\pm√(b^2-4ac))/(2a)=(-41\pm√(41^2-4(-16)(37)))/(2(-16))\\\\=(41\pm√(4049))/(32)\qquad\text{only $t>0$ is useful}`

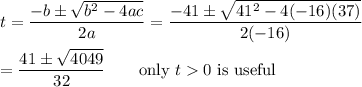
The exact landing time is (41+√4049)/32 seconds.

__

d) The highest point is at t=-b/(2a) = -41/(2(-16)) = 41/32 seconds.

The value of the function at that point is ...

h(41/32) = (-16(41/32) +41)(41/32) +37 = 41^2/64 +37 = 4049/64

The maximum height is 4049/64 = 63.265625 feet.

__

e) For a quadratic function, that average rate of change on an interval is the derivative at the midpoint of the interval. Here, the derivative is ...

h'(t) = -32t +41 . . . in feet per second

Then the average rates of change are ...

arc[1.5, 2] = h'(1.75) = -32·1.75 +41 = -15 ft/s

arc[2, 2.5] = h'(2.25) = -32(2.25) +41 = -31 ft/s

arc[2.5, 3] = h'(2.75) = -32(2.75) +41 = -47 ft/s

These are the average velocity of the water balloon over the given interval(s) in ft/s. Negative indicates downward.