Question

A 1285.0 kg car traveling initially with a speed of 25.000 m/s in an easterly direction crashes into the back of a 8 600.0 kg truck moving in the same direction at 20.000 m/s. The velocity of the car right after the collision is 18.000 m/s to the east.

A) What is the velocity of the truck right after the collision?
B) What is the change in mechanical energy of the car truck system in the collision?
C) Account for this change in mechanical energy.

Answer 1

Step-by-step explanation:

We have,

Mass of a car is 1285.0 kg

Initial speed of a car is 25 m/s in an easterly direction

Mass of a truck is 600 kg

Initial speed of a truck is 20 m/s

After the collision, final velocity of the car is 18 m/s

(A) Let
`v_2` is the velocity of velocity of the truck right after the collision. Using conservation of linear momentum. So,

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\\\v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2)\\\\v_2=(1285* 25+8600* 20-1285* 18)/(8600)\\\\v_2=21.04\ m/s`

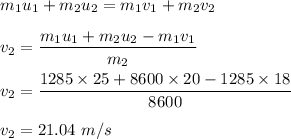
(B) Initial kinetic energy of truck car system :

`K_i=(1)/(2)(m_1u_1^2+m_2u_2^2)\\\\K_i=(1)/(2)(1285* (25)^2+8600* (20)^2)\\\\K_i=2121562.5\ J`

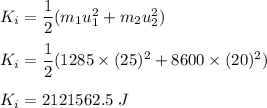
(C) Final kinetic energy of truck car system :

`K_f=(1)/(2)(m_1v_1^2+m_2v_2^2)\\\\K_f=(1)/(2)(1285* (18)^2+8600* (21.04)^2)\\\\K_f=2111700.88\ J`

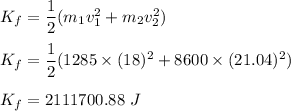
So, the change in kinetic energy is :

`\Delta K=K_f-K_i\\\\\Delta K=2111700.88-2121562.5\\\\\Delta K=9861.62\ J`

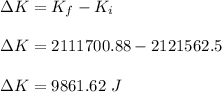
(C) The change in mechanical energy occurs when the energy gets converted in the form of heat and sound energy.