Question

As you know, a common example of a harmonic oscillator is a mass attached to a spring. In this problem, we will consider a horizontally moving block attached to a spring. Note that, since the gravitational potential energy is not changing in this case, it can be excluded from the calculations. For such a system, the potential energy is stored in the spring and is given by

U = 12k x 2
where k is the force constant of the spring and x is the distance from the equilibrium position. The kinetic energy of the system is, as always,
K = 12mv2
where m is the mass of the block and v is the speed of the block.
A) Find the total energy of the object at any point in its motion.
B) Find the amplitude of the motion.
C) Find the maximum speed attained by the object during its motion.

Answer 1

a)
`E = (1)/(2) \cdot k \cdot x^(2) + (1)/(2) \cdot m \cdot v^(2)`, b) Amplitude of the motion is
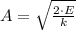`A = \sqrt{(2\cdot E)/(k) }`, c) The maximum speed attained by the object during its motion is
`v_(max) = \sqrt{(2\cdot E)/(m) }`.

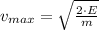Step-by-step explanation:

a) The total energy of the object is equal to the sum of potential and kinetic energies. That is:

`E = K + U`

Where:

`K` - Kinetic energy, dimensionless.

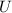`U` - Potential energy, dimensionless.

After replacing each term, the total energy of the object at any point in its motion is:

`E = (1)/(2) \cdot k \cdot x^(2) + (1)/(2) \cdot m \cdot v^(2)`

b) The amplitude of the motion occurs when total energy is equal to potential energy, that is, when objects reaches maximum or minimum position with respect to position of equilibrium. That is:

`E = U`

`E = (1)/(2) \cdot k \cdot A^(2)`

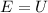
Amplitude is finally cleared:

`A = \sqrt{(2\cdot E)/(k) }`

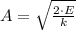
Amplitude of the motion is
`A = \sqrt{(2\cdot E)/(k) }`.

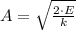c) The maximum speed of the motion when total energy is equal to kinetic energy. That is to say:

`E = K`

`E = (1)/(2)\cdot m \cdot v_(max)^(2)`

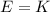
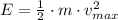
Maximum speed is now cleared:

`v_(max) = \sqrt{(2\cdot E)/(m) }`

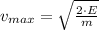
The maximum speed attained by the object during its motion is
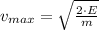`v_(max) = \sqrt{(2\cdot E)/(m) }`.