Answer:
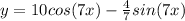
B.
B.
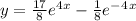
Explanation:
Question 1:
- We are given a homogeneous second order linear ODE as follows:
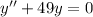
- A pair of independent functions are given as ( y1 ) and ( y2 ):
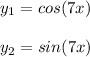
- The given ODE is subjected to following initial conditions as follows:
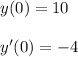
- We are to verify that the given independent functions ( y1 ) and ( y2 ) are indeed the solution to the given ODE. If the functions are solutions then find the complete solution of the homogeneous ODE of the form:
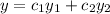
Solution:-
- To verify the functions are indeed the solution to the given ODE. We will plug the respective derivatives of each function [ y1 and y2 ] into the ODE and prove whether the equality holds true or not.
- Formulate the second derivatives of both functions y1 and y2 as follows:
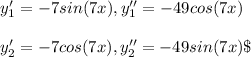
- Now plug the second derivatives of each function and the functions itself into the given ODE and verify whether the equality holds true or not.

- We see that both functions [ y1 and y2 ] holds true as the solution to the given homogeneous second order linear ODE. Hence, are the solution to given ODE.
- The complete solution to a homogeneous ODE is given in the form as follows:
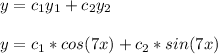
- To complete the above solution we need to determine the constants [ c1 and c2 ] using the initial conditions given. Therefore,

- Now we can write the complete solution to the given homogeneous second order linear ODE as follows:
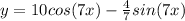 .... Answer
.... Answer
Question 2
- We are given a homogeneous second order linear ODE as follows:
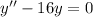
- A pair of independent functions are given as ( y1 ) and ( y2 ):
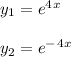
- The given ODE is subjected to following initial conditions as follows:

- We are to verify that the given independent functions ( y1 ) and ( y2 ) are indeed the solution to the given ODE. If the functions are solutions then find the complete solution of the homogeneous ODE of the form:
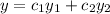
Solution:-
- To verify the functions are indeed the solution to the given ODE. We will plug the respective derivatives of each function [ y1 and y2 ] into the ODE and prove whether the equality holds true or not.
- Formulate the second derivatives of both functions y1 and y2 as follows:
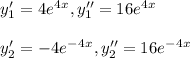
- Now substitute the second derivatives of each function and the functions itself into the given ODE and verify whether the equality holds true or not.
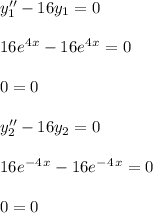
- We see that both functions [ y1 and y2 ] holds true as the solution to the given homogeneous second order linear ODE. Hence, are the solution to given ODE.
- The complete solution to a homogeneous ODE is given in the form as follows:
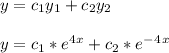
- To complete the above solution we need to determine the constants [ c1 and c2 ] using the initial conditions given. Therefore,
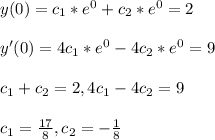
- Now we can write the complete solution to the given homogeneous second order linear ODE as follows:
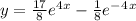 .... Answer
.... Answer