Answer:
The p-value of the test is 0.1515.
Explanation:
The hypothesis for the test can be defined as follows:
H₀: The mean level of arsenic is 80 ppb, i.e. μ = 80.
Hₐ: The mean level of arsenic is greater than 80 ppb, i.e. μ > 80.
As the population standard deviation is not known we will use a t-test for single mean.
It is provided that the sample mean was,
 .
.
The adjusted sample provided is:
S = {57, 64, 70, 82, 84, 123}
Compute the sample standard deviation as follows:
![\bar x=\farc{57+64+70+82+84+123}{6}=80\\\\s=\sqrt{(1)/(6-1)* [(57-80)^(2)+(64-80)^(2)+(70-80)^(2)+...+(123-80)^(2)]}=23.47](https://img.qammunity.org/2021/formulas/mathematics/college/orrp3z2jove4tud7406s457bmpwx3y4zce.png)
Compute the test statistic value as follows:
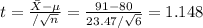
Thus, the test statistic value is 1.148.
Compute the p-value of the test as follows:
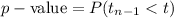

*Use a t-table.
Thus, the p-value of the test is 0.1515.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.
p-value = 0.1515 > α = 0.05
The null hypothesis will not be rejected at 5% level of significance.
Thus, concluding that the mean level of arsenic in chicken from the suppliers is 80 ppb.